Why Physics Models?

Matthew Daigle,
Matt is a Principal PdM Scientist at Novity
What is a Physics Model and Why Does it Matter to Predictive Maintenance?
Any solution to predictive maintenance (PdM) must answer two key questions for any monitored equipment: what is the current health, and when will it fail? Approaches to answer these questions generally fall into either data-driven approaches that utilize machine learning, model-based approaches that rely on building physics models of equipment behavior, or hybrid approaches, leveraging a combination of machine learning and model-based approaches.
Why do we use physics models, and why are they key to accurate PdM solutions?
Many PdM methods are purely data-driven and rely on training models to estimate health and predict failure through machine learning. These solutions encounter three fundamental problems:
- Generalizability: Without a large amount and a wide variety of data, trained models may not generalize to other instances of the same equipment or a change in operating conditions. This makes it difficult to scale such solutions without costly model retraining.
- Data scarcity: For industrial use cases, the right data needed to train PdM models, especially failure data, is not widely available. Without failure data, machine learning models cannot be developed to either recognize when a component has failed or to predict its failure.
- Explainability: Machine learning models are often black boxes. It is difficult to understand why they are making the predictions that they are making, and therefore it is hard to explain their outputs.
On the other hand, physics models are developed using well-known fundamental physical principles and equations that take into account how equipment operates, both in nominal and degraded conditions and within different operating conditions. A physics-based algorithm will use the model to infer current equipment health through the available sensor data. Using physics-of-failure models, physics-based algorithms can infer how equipment is degrading over time as a function of operating conditions and predict how this degradation will eventually lead to equipment failure.
In contrast to machine learning models, which must learn domain knowledge through vast amounts of data, physics models already have this knowledge embedded in the form of mathematical equations that relate physical behavior with applied loads and operating conditions, and, therefore, require significantly less data to develop and validate. These models naturally describe how equipment behavior will change across a wide range of operation and throughout different levels of degradation. Put in another way: they are generalizable. Further, even if failure data is unavailable, in which case machine learning cannot be applied, physics models provide a solution when the physics of failure are well-understood. This alleviates the data scarcity problem. Finally, since knowledge about equipment behavior is captured through physics equations, it is trivial to interrogate these models and explain the behavior of algorithms based on them in a physically meaningful way.
From theory to practice
As an example, let's take a centrifugal pump. A common way to investigate the performance of a pump is to look at its pump curve. The pump curve describes the relationship between the total pressure, or head, produced by the pump and the flow through the pump. Through physics modeling, we can determine what this relationship looks like and how it will likely change as the pump degrades.
The first figure shows how the pump curve changes from that of a healthy pump to increasing levels of impeller erosion – for instance as a result of cavitation. The second figure shows how the pump curve changes from a healthy pump to increasing levels of internal leakage. In both cases, physics models can tell us how an observed pump curve maps onto different degradation levels, thus providing an estimate of pump health.
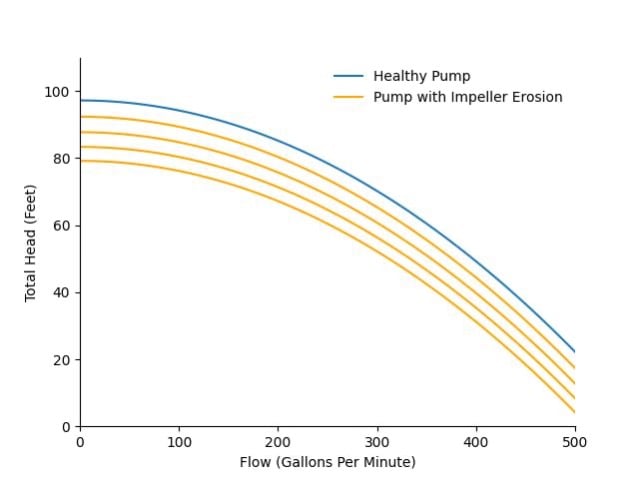
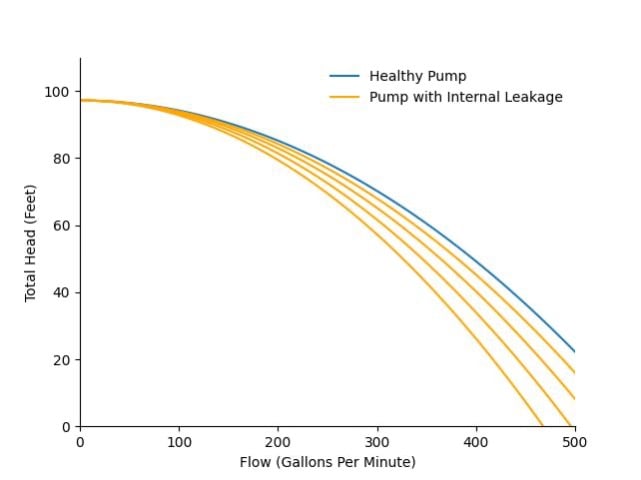
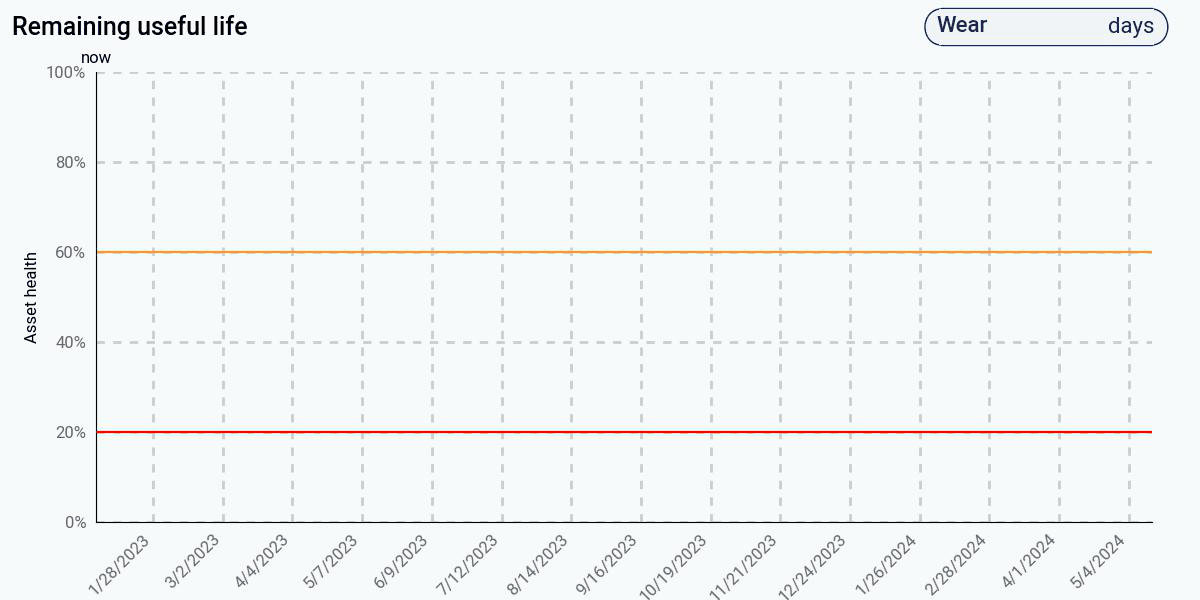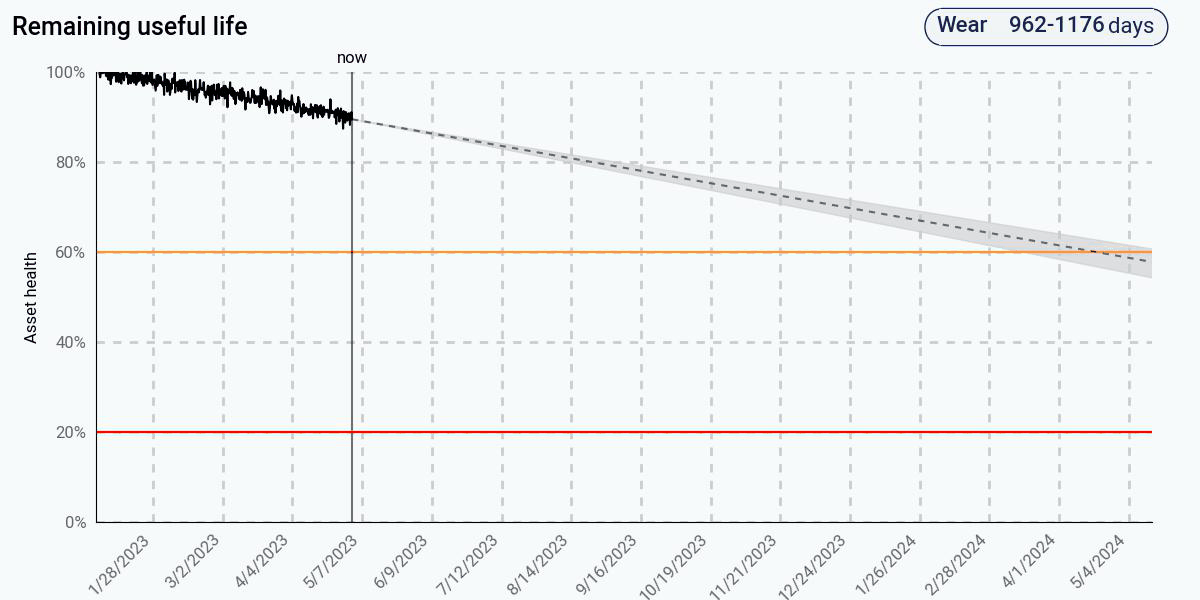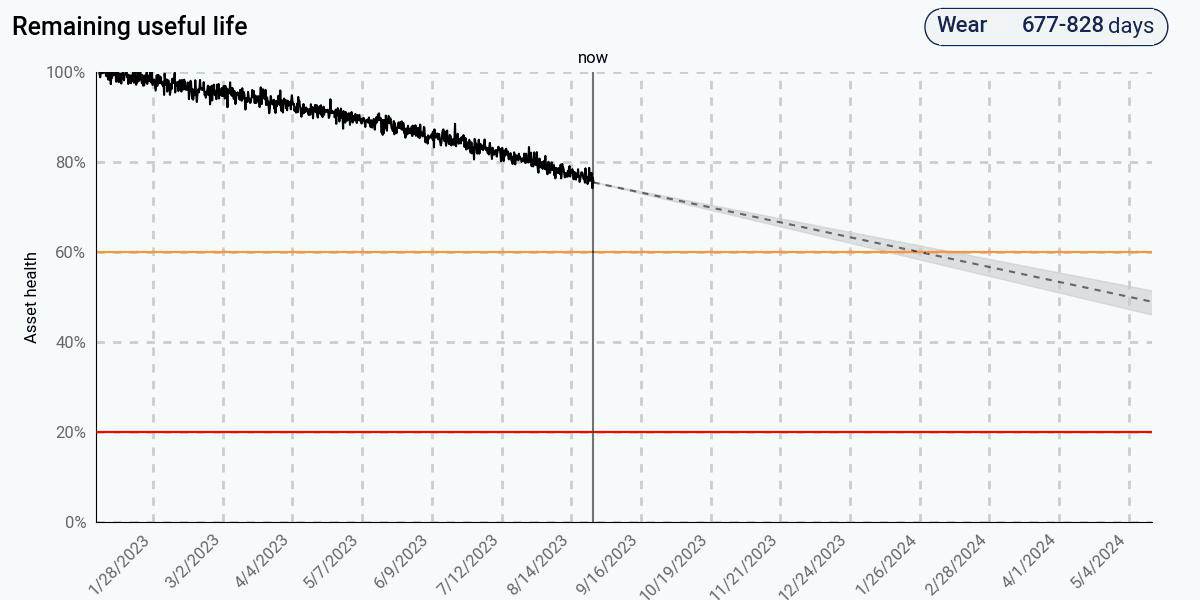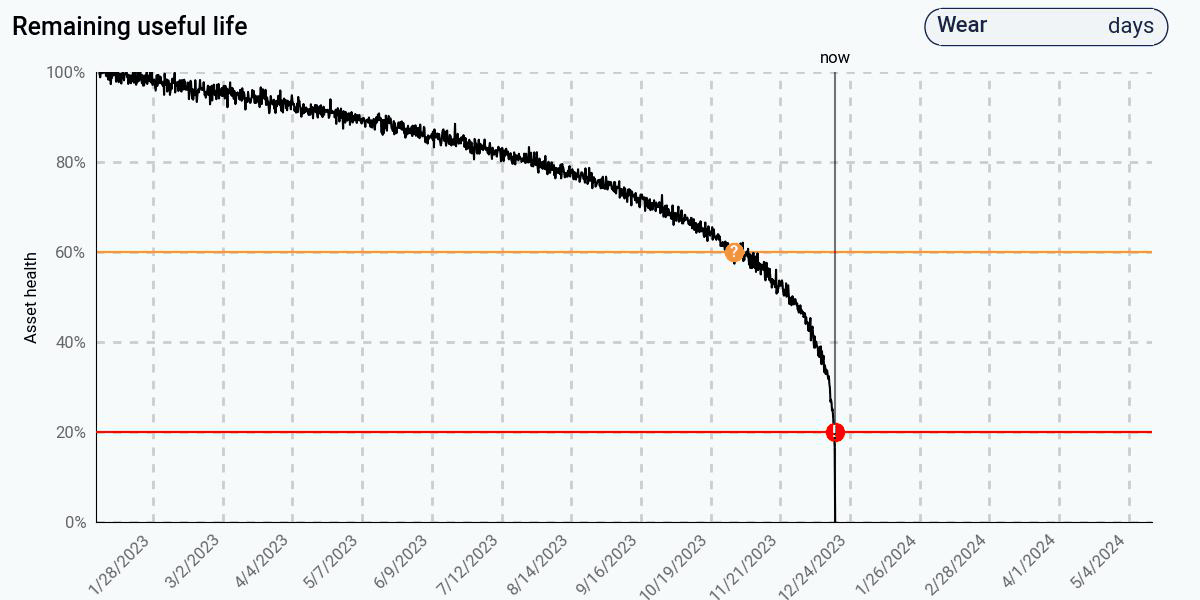
To see what this looks like in practice, let’s compare three common approaches: (1) a data-driven trending algorithm based on linear regression, (2) a more sophisticated data-driven algorithm with adaptive trending, and (3) a physics-based algorithm for remaining life prediction on this pump. The figures below show the health estimate over time, and the gray and red areas represent the algorithm’s prediction of the end of life and its uncertainty.
The first figure shows the predictions from the trending algorithm. This algorithm fits a line to the health to determine when health goes to zero. Initially, the health looks linear, and this algorithm produces a sensible result. However, as health continues to degrade, the degradation is clearly nonlinear. At 60% health, remaining life is still predicted to be well over a year. At 20% health, remaining life is still predicted to be about a year despite the clear downward trend in health.
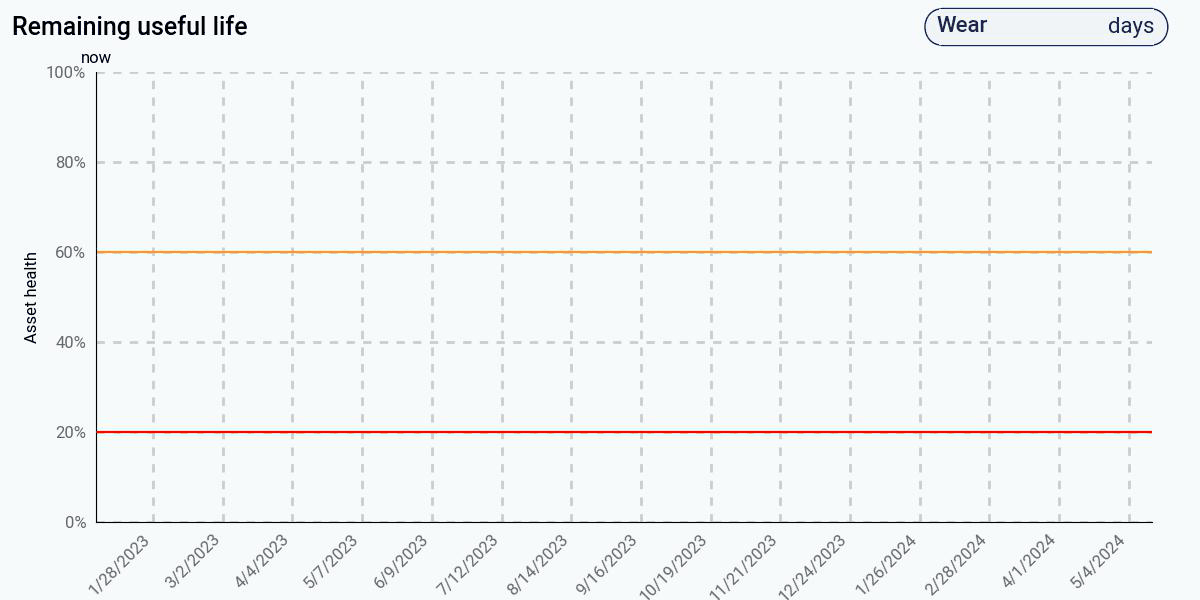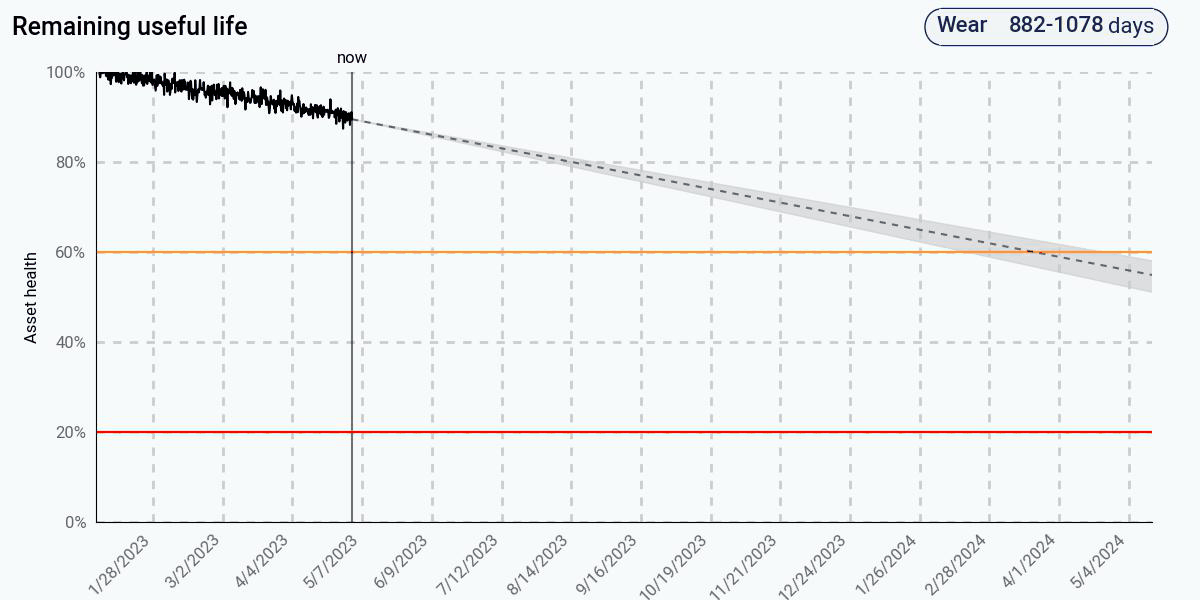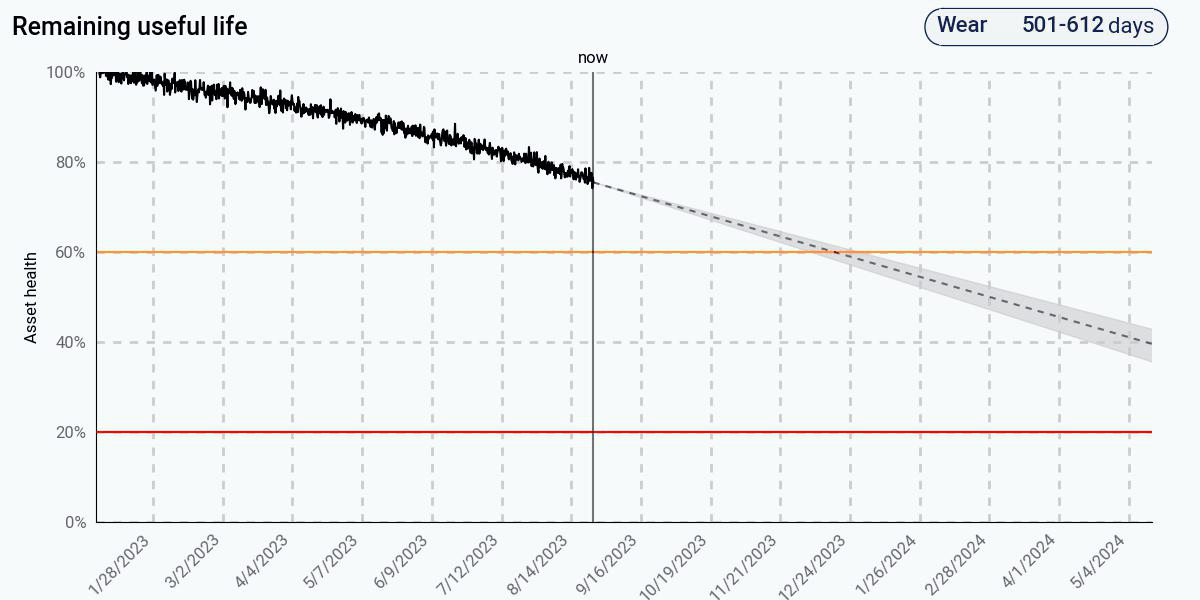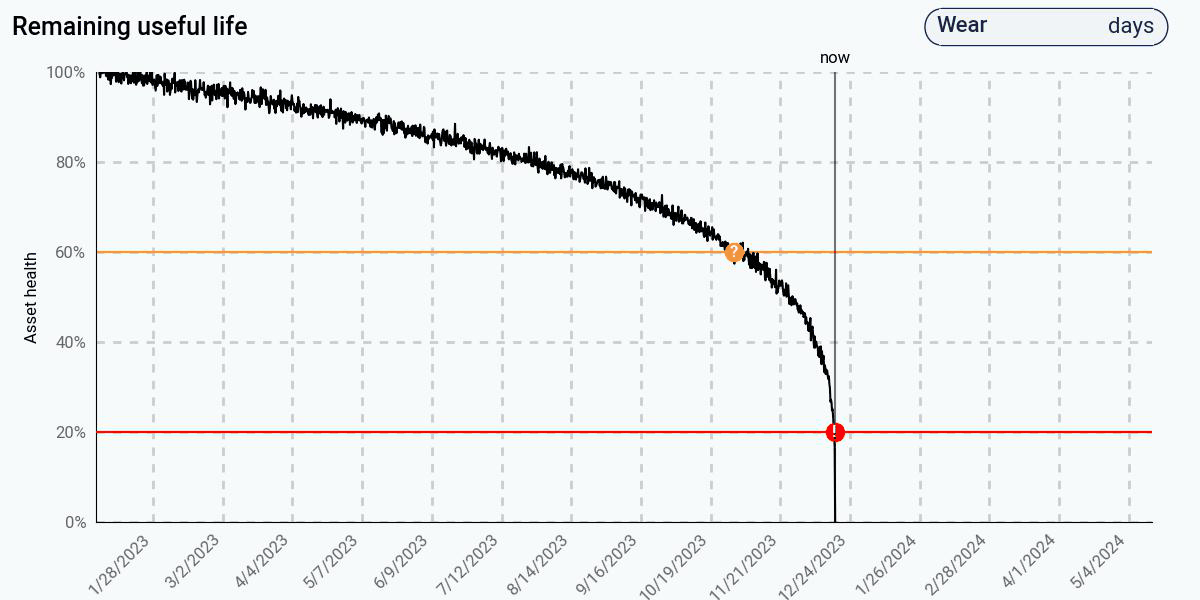
The adaptive data-driven approach improves on the simple trending approach by assuming that the current health degradation rate will continue in the future. Initially, when the health degrades linearly, its predictions match those of the trending-based approach, since there is no indication in the data that there is any nonlinearity. Once the nonlinear behavior appears, the predictions adjust and begin to get more accurate, and eventually come pretty close to the actual end of life. At 20% health, remaining life is predicted to be about a month.
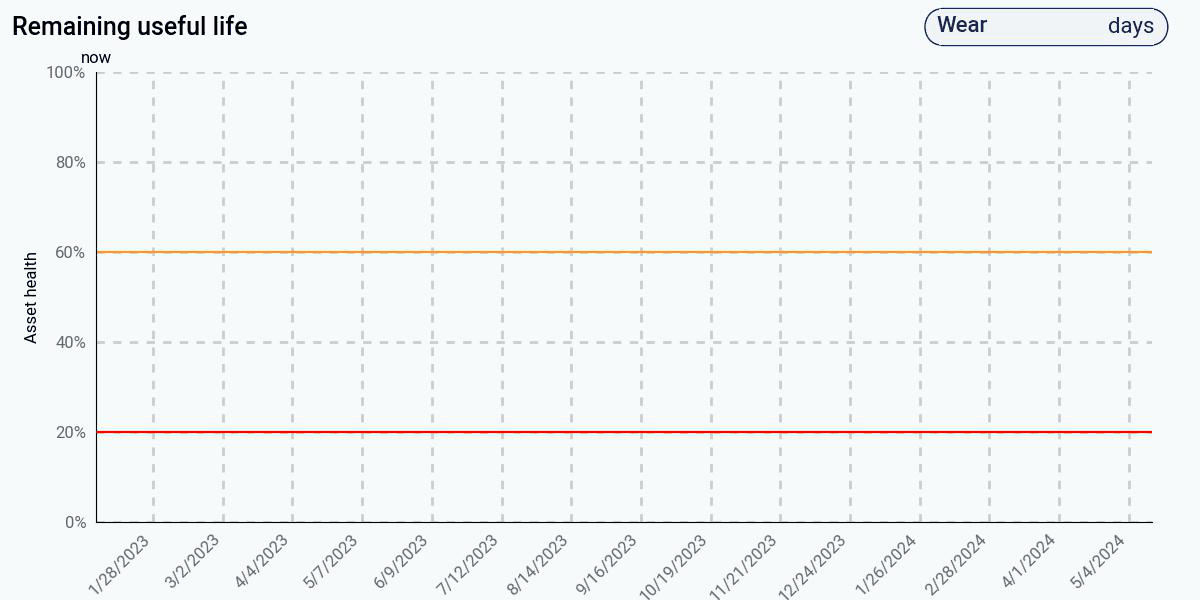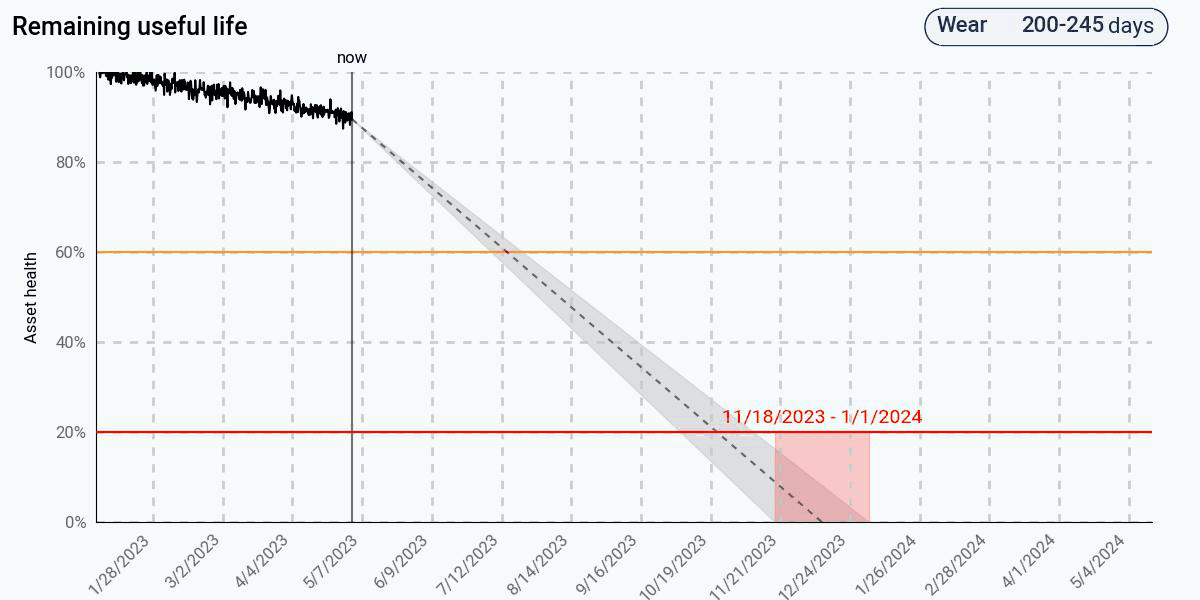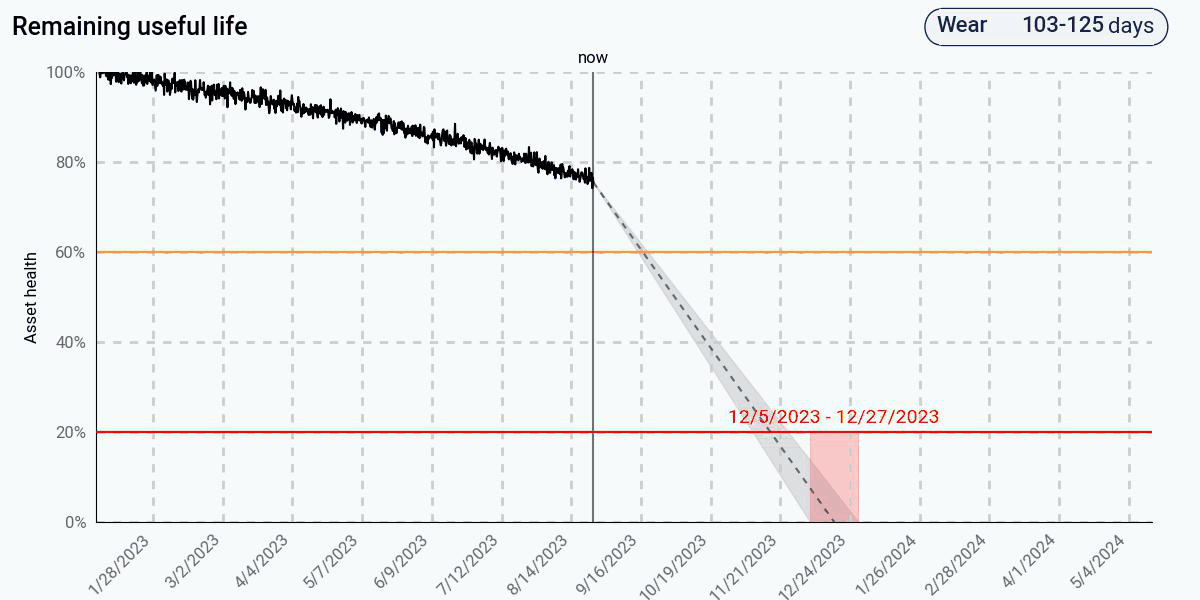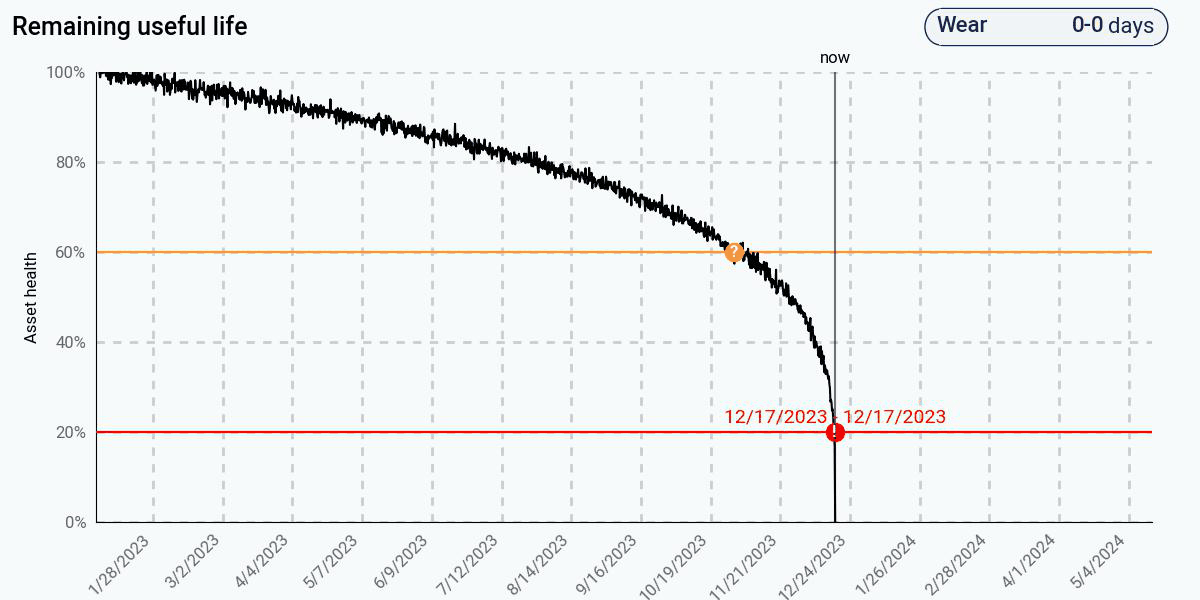
In contrast, the physics-based approach, using the same health data, predicts early that end of life will occur in less than one year. This is because the physics model understands that the degradation will actually be nonlinear, despite what the initial data seems to suggest. The physics model has encoded the knowledge that, as degradation increases, the rate of degradation itself will increase, leading to an exponentially decreasing health curve. At 60% health, the predicted remaining life is a little over a month – much more accurate than the data-driven approaches. At 20% health, it correctly predicts that the remaining life is less than one day.
Despite having a data-driven approach that recognizes and adapts to the change in the health curve, the advantages of the physics-based approach are clear: predictions are significantly more accurate, and accurate predictions are available much earlier, and with less data than a comparably accurate data-driven approach.
Summary
To summarize, physics models offer several advantages over purely data-driven approaches. They incorporate existing engineering knowledge in the form of mathematical models, enable timely and accurate remaining life predictions with less data, and their results are explainable.
Reach out
If you're interested in learning more, contact us! We'd love to talk about how physics-based models can help improve your PdM performance.


